Fit Generalised Additive Models (GAMs) to the Dispersal Data

A.H. Sparks

2024-05-04

Source: vignettes/a05_GAM.Rmd

Import Data

Create Data Set for GAMs

Join the lesion_counts data and the summary_weather data to create dat for creating GAMs.

dat <-
   left_join(lesion_counts, summary_weather, by = c("site", "rep"))

Fit GAMs

For reproducibility purposes, use set.seed().

mod1 - s(Distance) 

mod1 <-
   gam(
      m_lesions ~ s(distance, k = 5),
      data = dat
   )

summary(mod1)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ s(distance, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.08024    0.04751   22.74   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df    F p-value    
## s(distance) 3.926  3.996 78.4  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.482   Deviance explained = 48.8%
## GCV = 0.76522  Scale est. = 0.75394   n = 334
print(p_gam(x = getViz(mod1)) +
         ggtitle("s(Distance)"),
      pages = 1)

mod2 - s(Distance) + Precipitation 

mod2 <-
   gam(
      m_lesions ~ sum_rain+ s(distance, k = 5),
      data = dat
   )

summary(mod2)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ sum_rain + s(distance, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.772464   0.092471   8.354 1.89e-15 ***
## sum_rain    0.031885   0.008278   3.852 0.000141 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.928  3.996 81.76  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.502   Deviance explained =   51%
## GCV = 0.7366  Scale est. = 0.72352   n = 334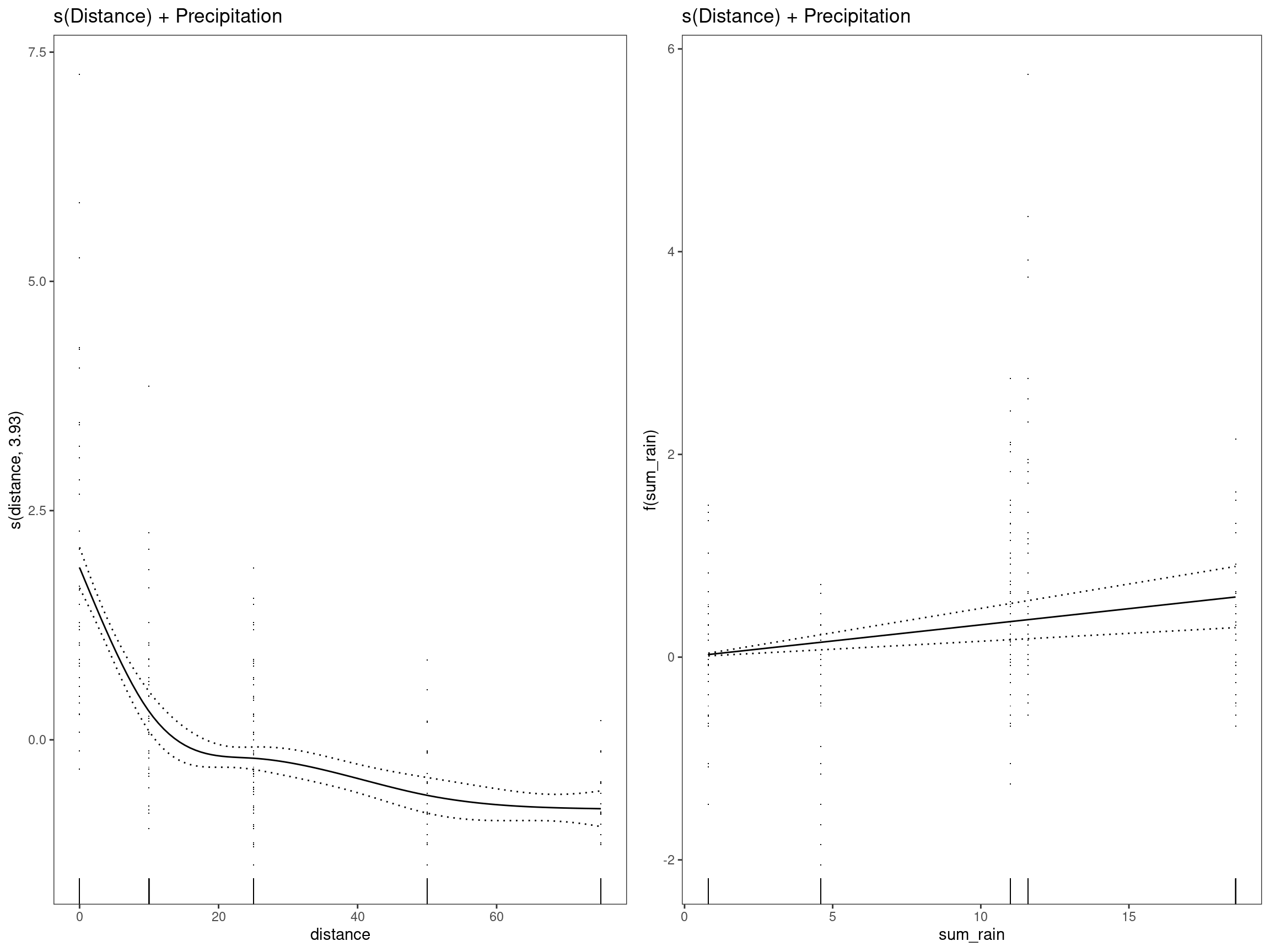
print(p_gam(x = getViz(mod2)) +
         ggtitle("s(Distance) + Precipitation"),
      pages = 1)

mod3 - s(Distance) + Wind speed 

mod3 <-
   gam(m_lesions ~ mws + s(distance, k = 5),
       data = dat)

summary(mod3)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ mws + s(distance, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  0.64401    0.11825   5.446 1.01e-07 ***
## mws          0.12273    0.03059   4.012 7.47e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.929  3.996 81.99  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.504   Deviance explained = 51.2%
## GCV = 0.73389  Scale est. = 0.72086   n = 334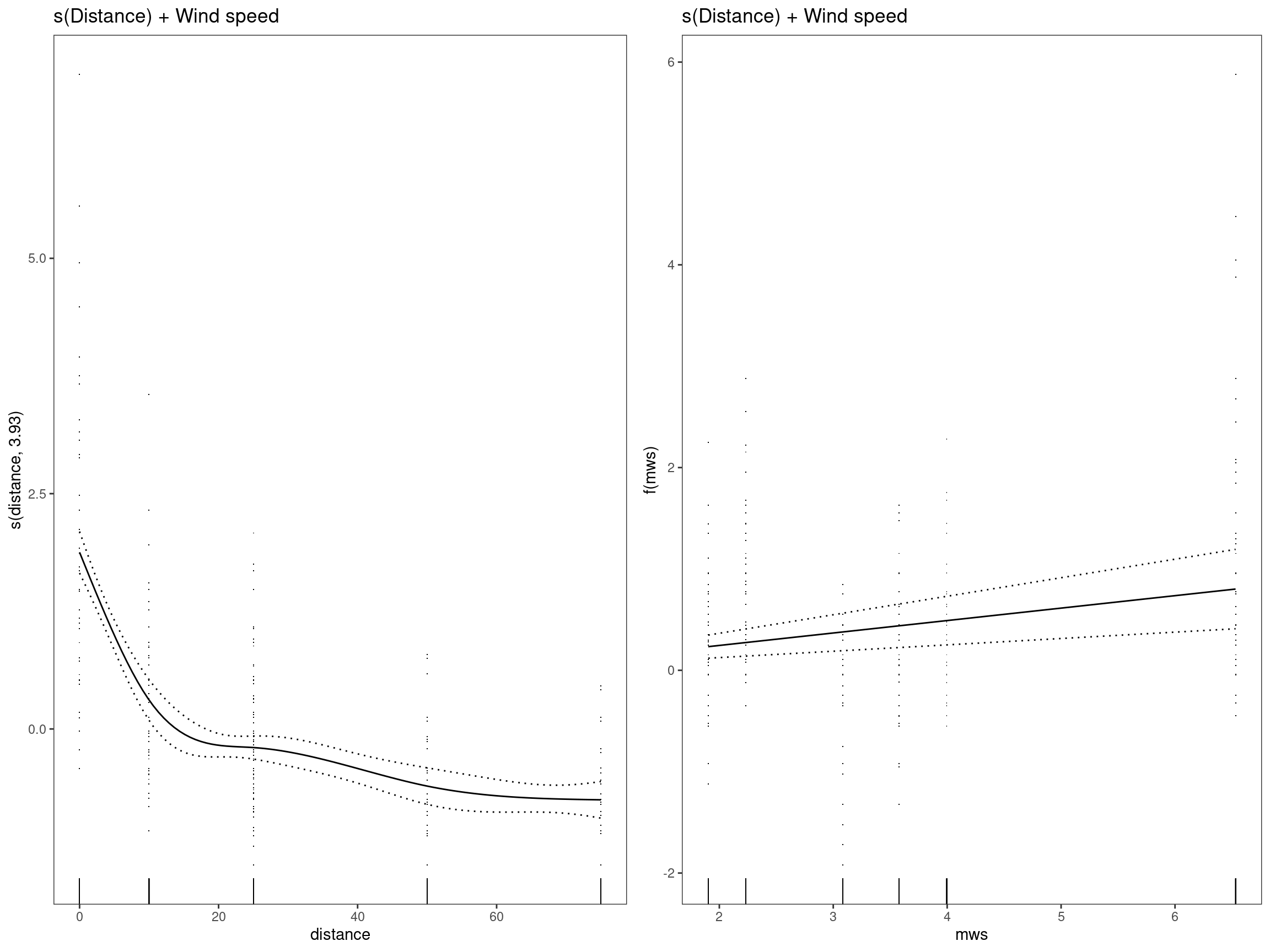
print(p_gam(x = getViz(mod3)) +
         ggtitle("s(Distance) + Wind speed"),
      pages = 1)

mod4 - s(Distance) + Wind speed + Precipitation 

mod4 <-
   gam(m_lesions ~ sum_rain + mws + s(distance, k = 5),
       data = dat)

summary(mod4)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ sum_rain + mws + s(distance, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.435675   0.132265   3.294 0.001096 ** 
## sum_rain    0.027392   0.008239   3.325 0.000986 ***
## mws         0.106960   0.030507   3.506 0.000518 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.931  3.996 84.56  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.519   Deviance explained = 52.8%
## GCV = 0.71426  Scale est. = 0.69944   n = 334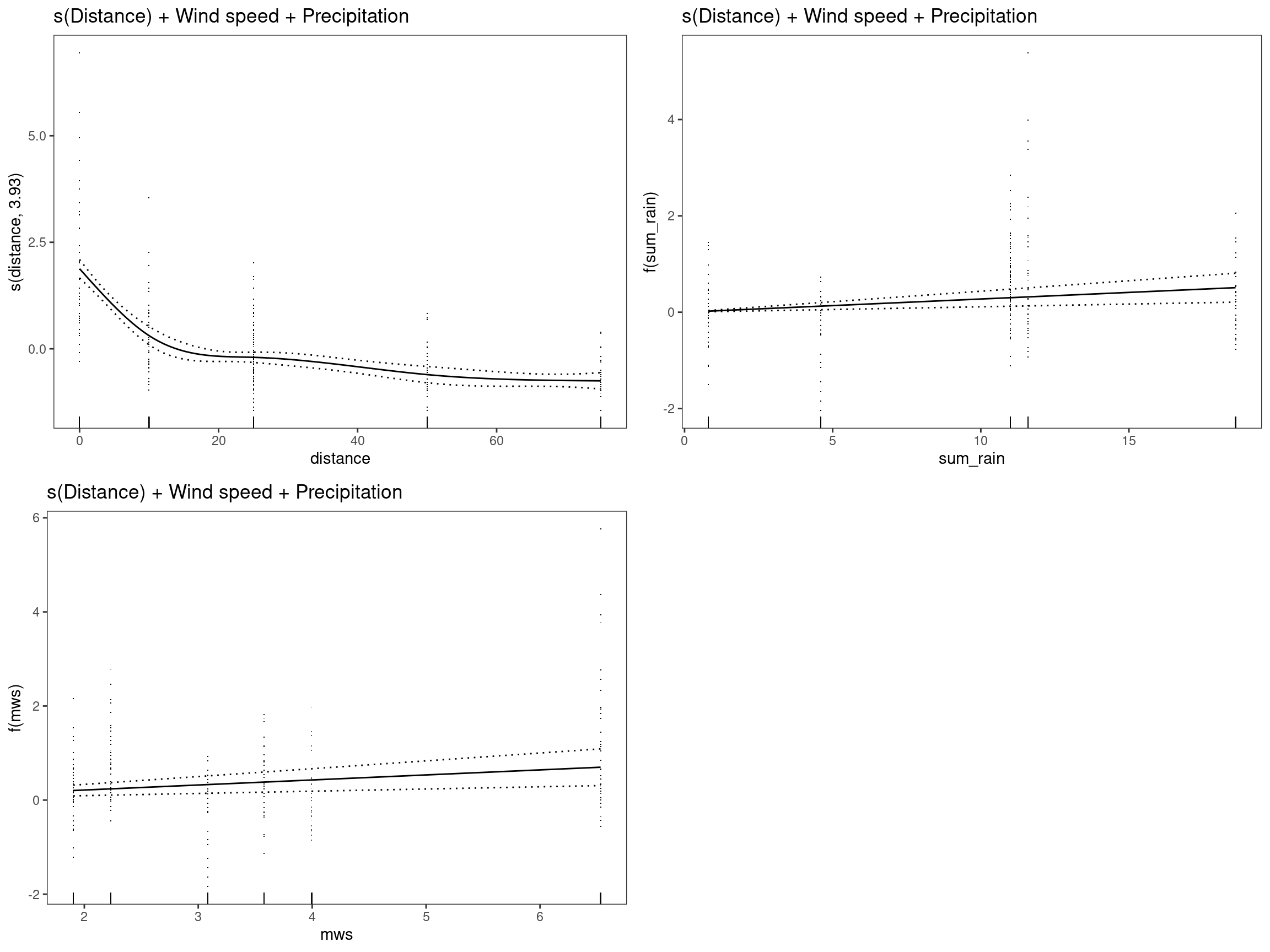
print(p_gam(x = getViz(mod4)) +
         ggtitle("s(Distance) + Wind speed + Precipitation"),
      pages = 1)

mod5 - s(Distance + Wind Speed) + Precipitation 

mod5 <-
   gam(
      m_lesions ~ sum_rain + s(distance + mws, k = 5),
      data = dat
   )
## Warning in term[i] <- attr(terms(reformulate(term[i])), "term.labels"): number
## of items to replace is not a multiple of replacement length
summary(mod5)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ sum_rain + s(distance + mws, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 0.772464   0.092471   8.354 1.89e-15 ***
## sum_rain    0.031885   0.008278   3.852 0.000141 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.928  3.996 81.76  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.502   Deviance explained =   51%
## GCV = 0.7366  Scale est. = 0.72352   n = 334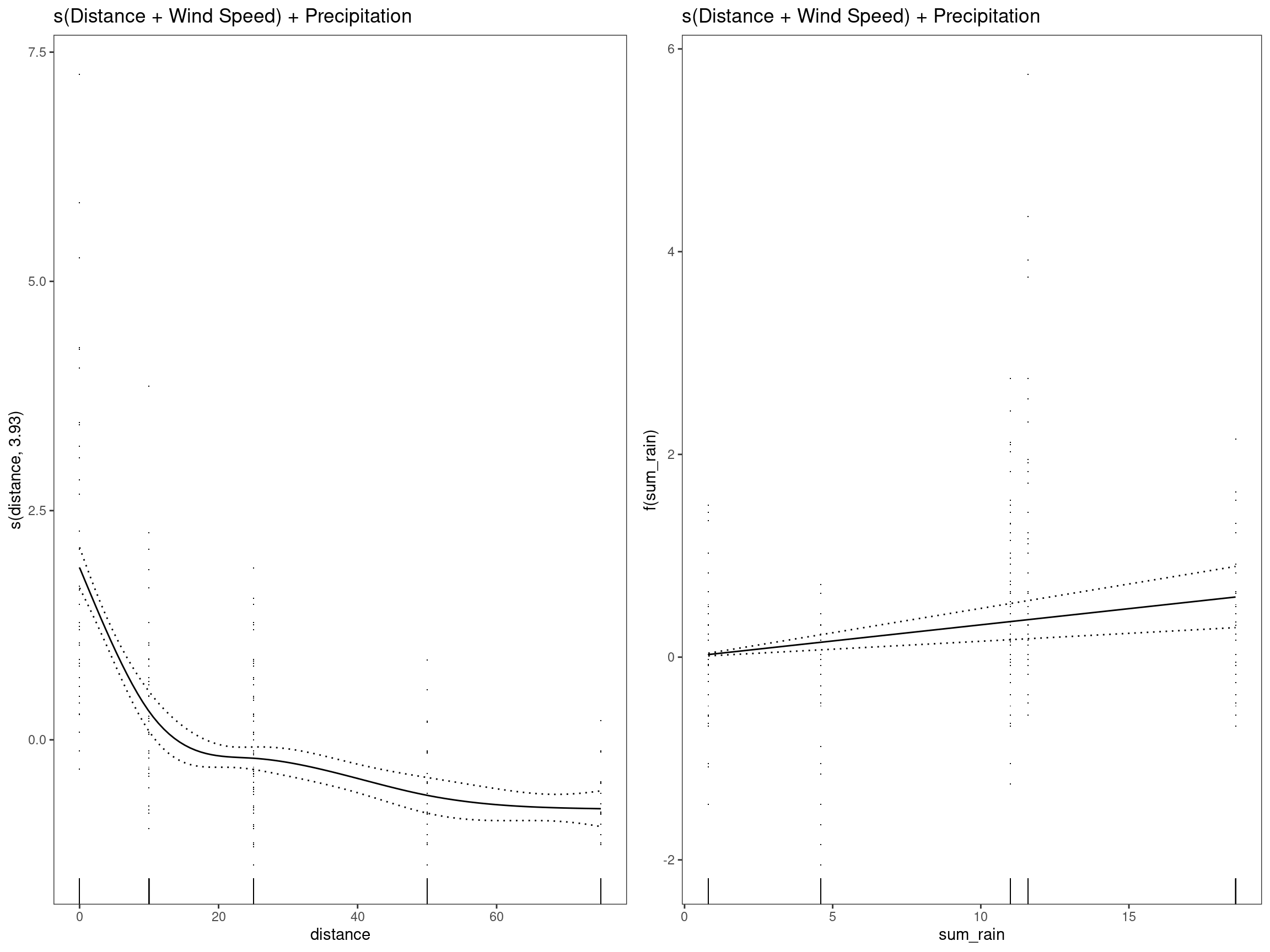
print(p_gam(x = getViz(mod5)) +
         ggtitle("s(Distance + Wind Speed) + Precipitation"),
      pages = 1)

mod6 - s(Distance) + s(Wind Speed) + Precipitation 

mod6 <-
   gam(
      m_lesions ~ sum_rain + s(distance, k = 5) + s(mws, k = 5),
      data = dat
   )

summary(mod6)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ sum_rain + s(distance, k = 5) + s(mws, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.40355    0.18004   7.796 8.82e-14 ***
## sum_rain    -0.03349    0.01810  -1.850   0.0652 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.938  3.997 93.81  <2e-16 ***
## s(mws)      3.926  3.995 12.66  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.566   Deviance explained = 57.8%
## GCV = 0.6497  Scale est. = 0.63051   n = 334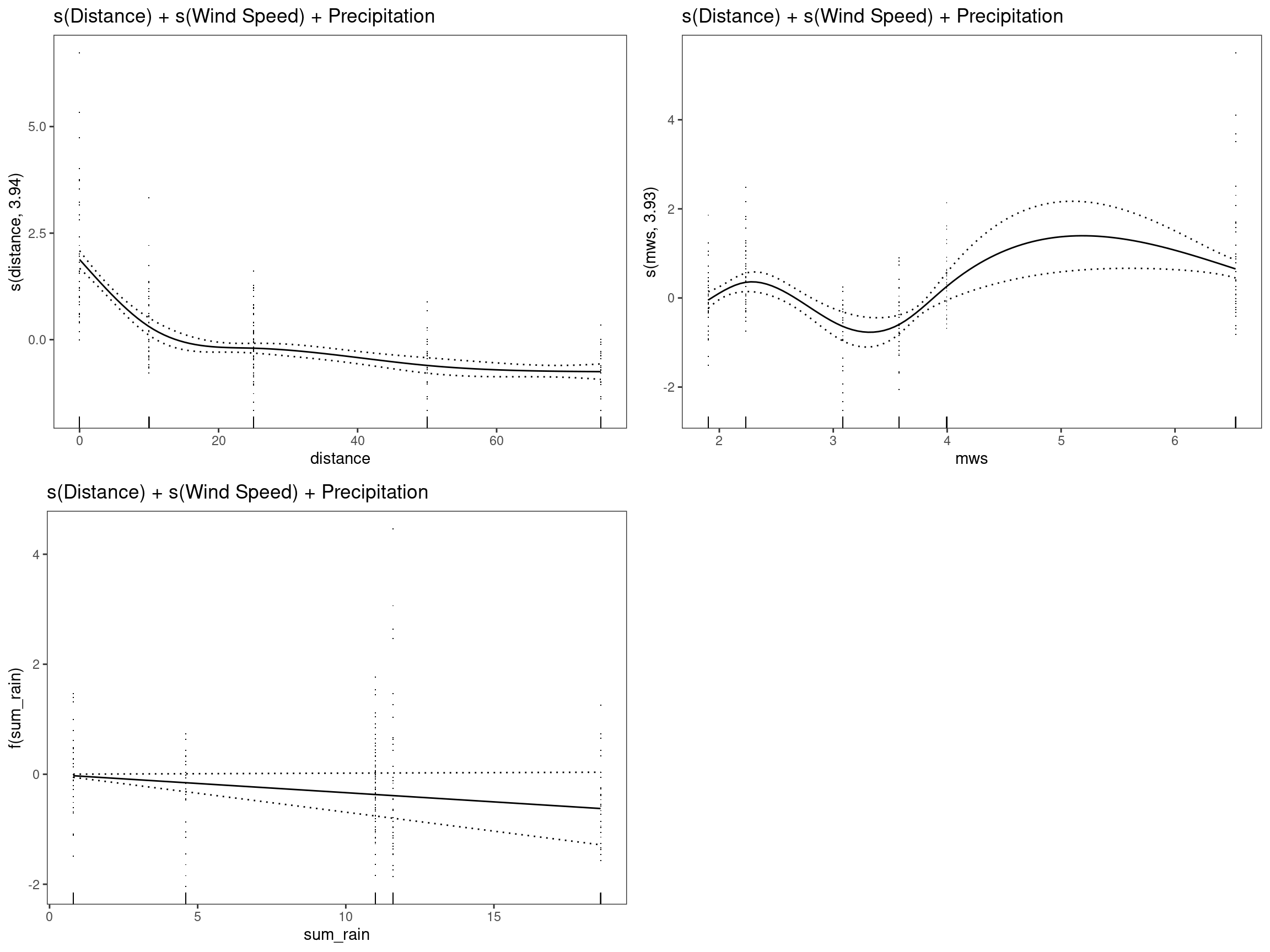
print(p_gam(x = getViz(mod6)) +
         ggtitle("s(Distance) + s(Wind Speed) + Precipitation"),
      pages = 1)

mod7 - s(Distance) + s(Wind Speed) 

mod7 <-
   gam(
      m_lesions ~ s(distance, k = 5) + s(mws, k = 5),
      data = dat
   )

summary(mod7)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ s(distance, k = 5) + s(mws, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.08024    0.04366   24.74   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.937  3.997 92.96  <2e-16 ***
## s(mws)      3.917  3.995 16.04  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.562   Deviance explained = 57.3%
## GCV = 0.65392  Scale est. = 0.63659   n = 334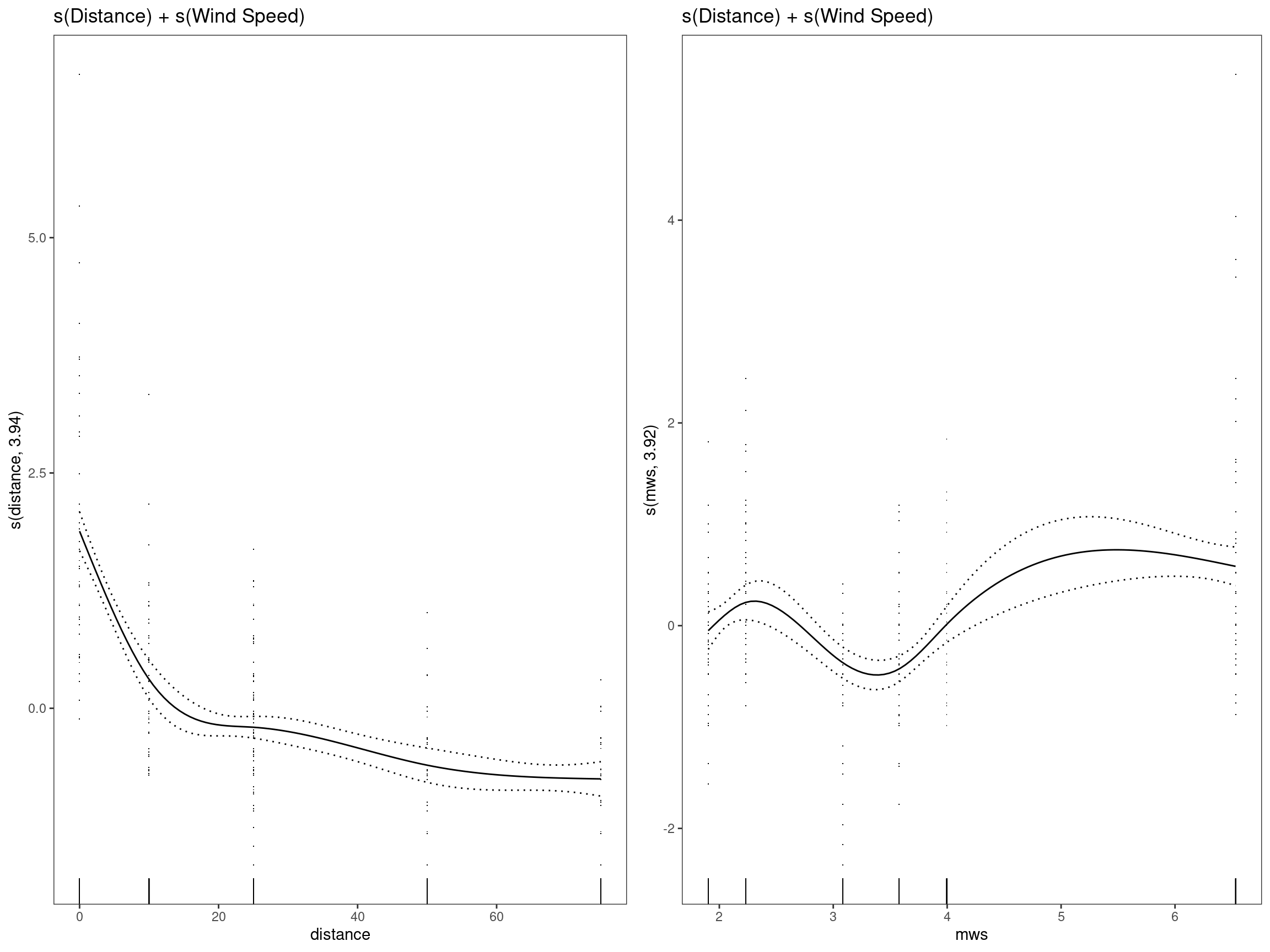
print(p_gam(x = getViz(mod7)) +
         ggtitle("s(Distance) + s(Wind Speed)"),
      pages = 1)

mod8 - s(Distance) + s(Wind Speed) + s(Precipitation) 

mod8 <-
   gam(
      m_lesions ~ s(distance, k = 5) + s(mws, k = 5) + s(sum_rain, k = 5),
      data = dat
   )

summary(mod8)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ s(distance, k = 5) + s(mws, k = 5) + s(sum_rain, 
##     k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.08024    0.04345   24.86   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df      F p-value    
## s(distance) 3.938  3.997 93.805  <2e-16 ***
## s(mws)      1.666  1.761  1.356  0.3404    
## s(sum_rain) 3.192  3.219  3.298  0.0113 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.566   Deviance explained = 57.8%
## GCV = 0.64956  Scale est. = 0.63051   n = 334
print(p_gam(x = getViz(mod8)) +
         ggtitle("s(Distance) + s(Wind Speed) + s(Precipitation)"),
      pages = 1)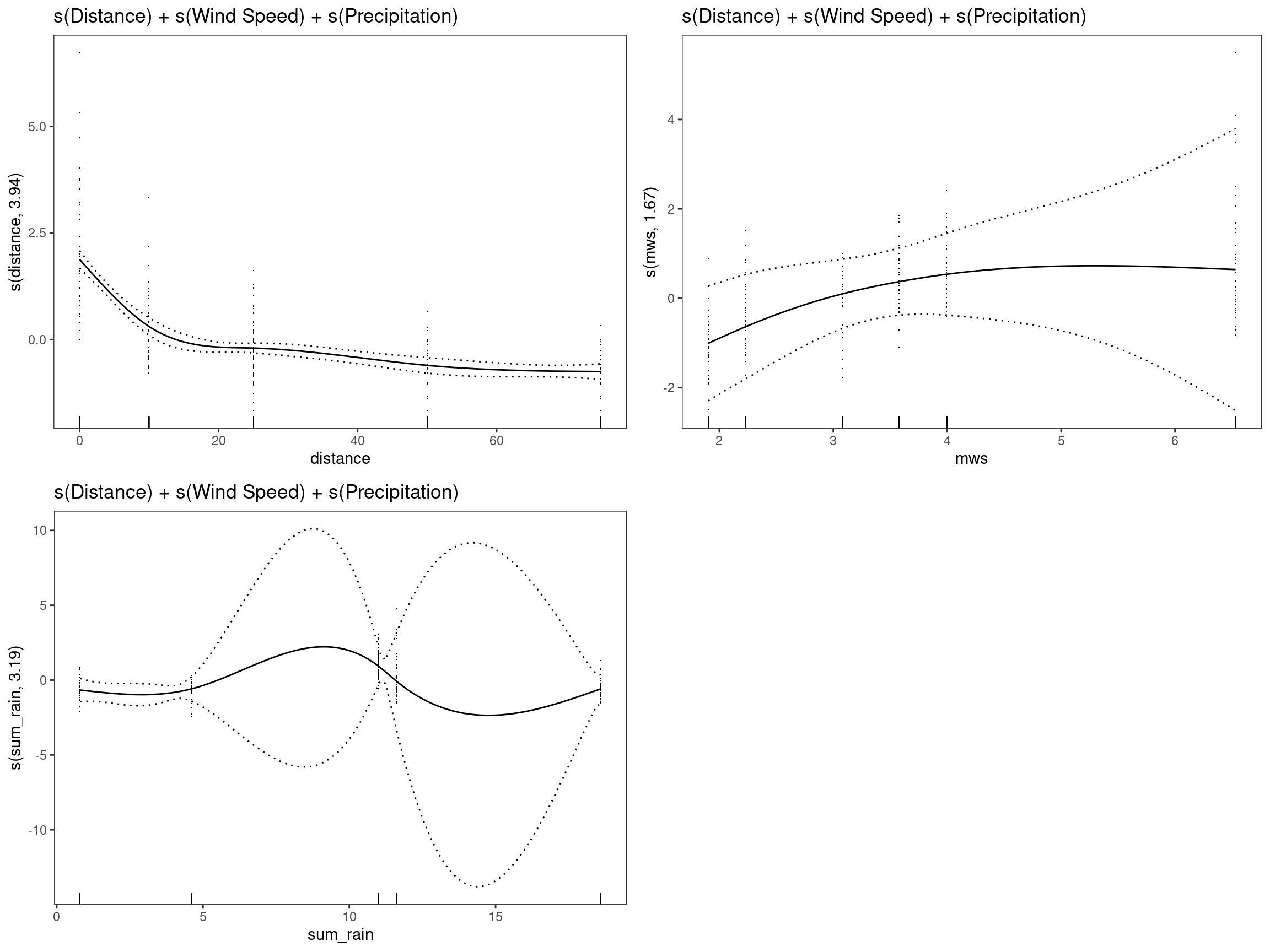

mod9 - s(Distance) + s(Precipitation) 

mod9 <-
   gam(
      m_lesions ~ s(distance, k = 5) + s(sum_rain, k = 5),
      data = dat
   )

summary(mod9)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ s(distance, k = 5) + s(sum_rain, k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  1.08024    0.04393   24.59   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.936  3.997 91.78  <2e-16 ***
## s(sum_rain) 3.901  3.991 15.19  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.557   Deviance explained = 56.7%
## GCV = 0.66195  Scale est. = 0.64444   n = 334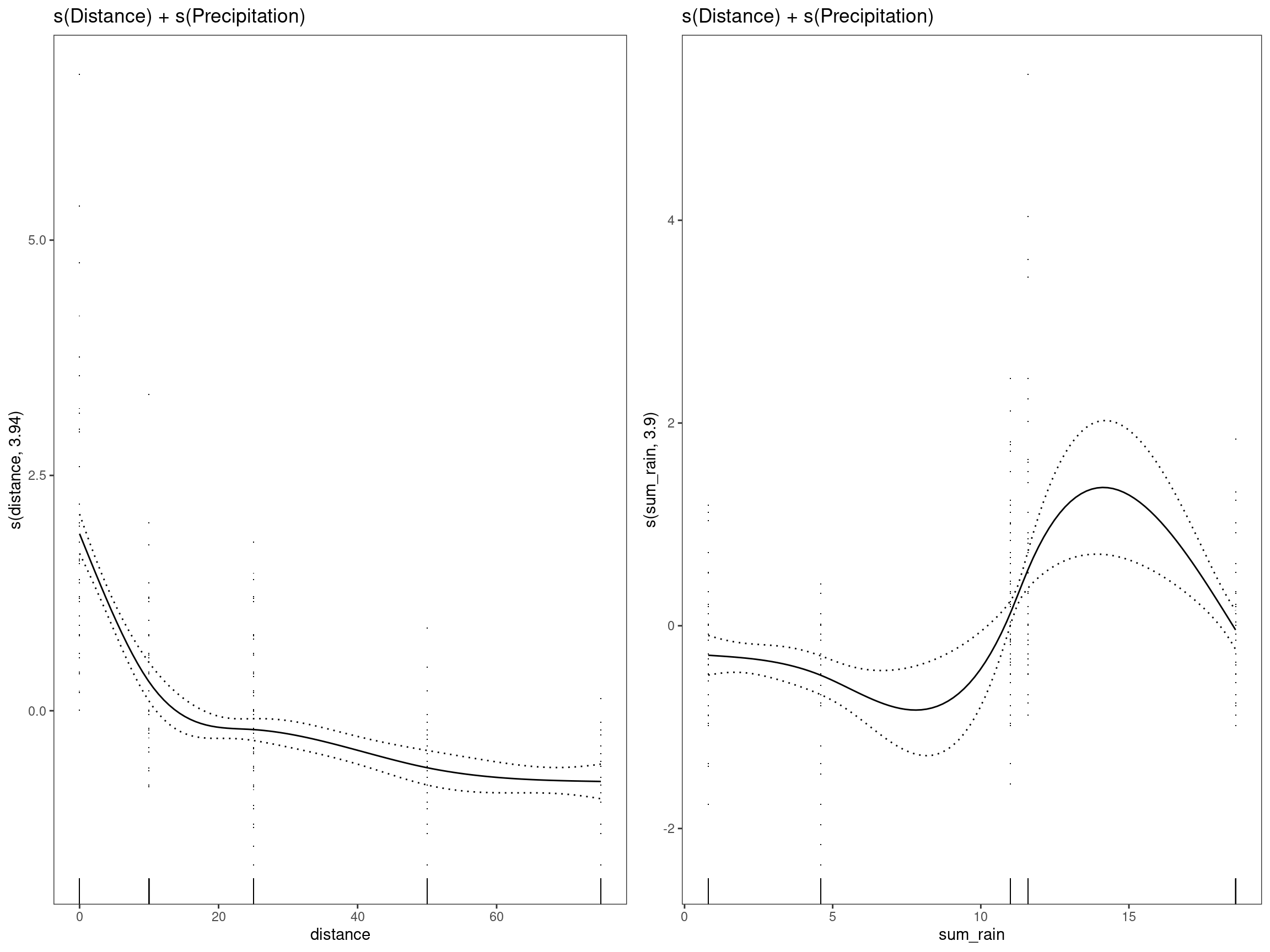
print(p_gam(x = getViz(mod9)) +
         ggtitle("s(Distance) + s(Precipitation)"),
      pages = 1)

mod10 - s(Distance) +s(Precipitation) + Wind speed 

mod10 <-
   gam(
      m_lesions ~ s(distance, k = 5) + s(sum_rain, k = 5) + mws,
      data = dat
   )

summary(mod10)
## 
## Family: gaussian 
## Link function: identity 
## 
## Formula:
## m_lesions ~ s(distance, k = 5) + s(sum_rain, k = 5) + mws
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)  -2.5358     1.4136  -1.794   0.0738 .
## mws           1.0174     0.3975   2.559   0.0109 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df     F p-value    
## s(distance) 3.937  3.997 93.76  <2e-16 ***
## s(sum_rain) 3.764  3.944 13.68  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.566   Deviance explained = 57.8%
## GCV = 0.64968  Scale est. = 0.63081   n = 334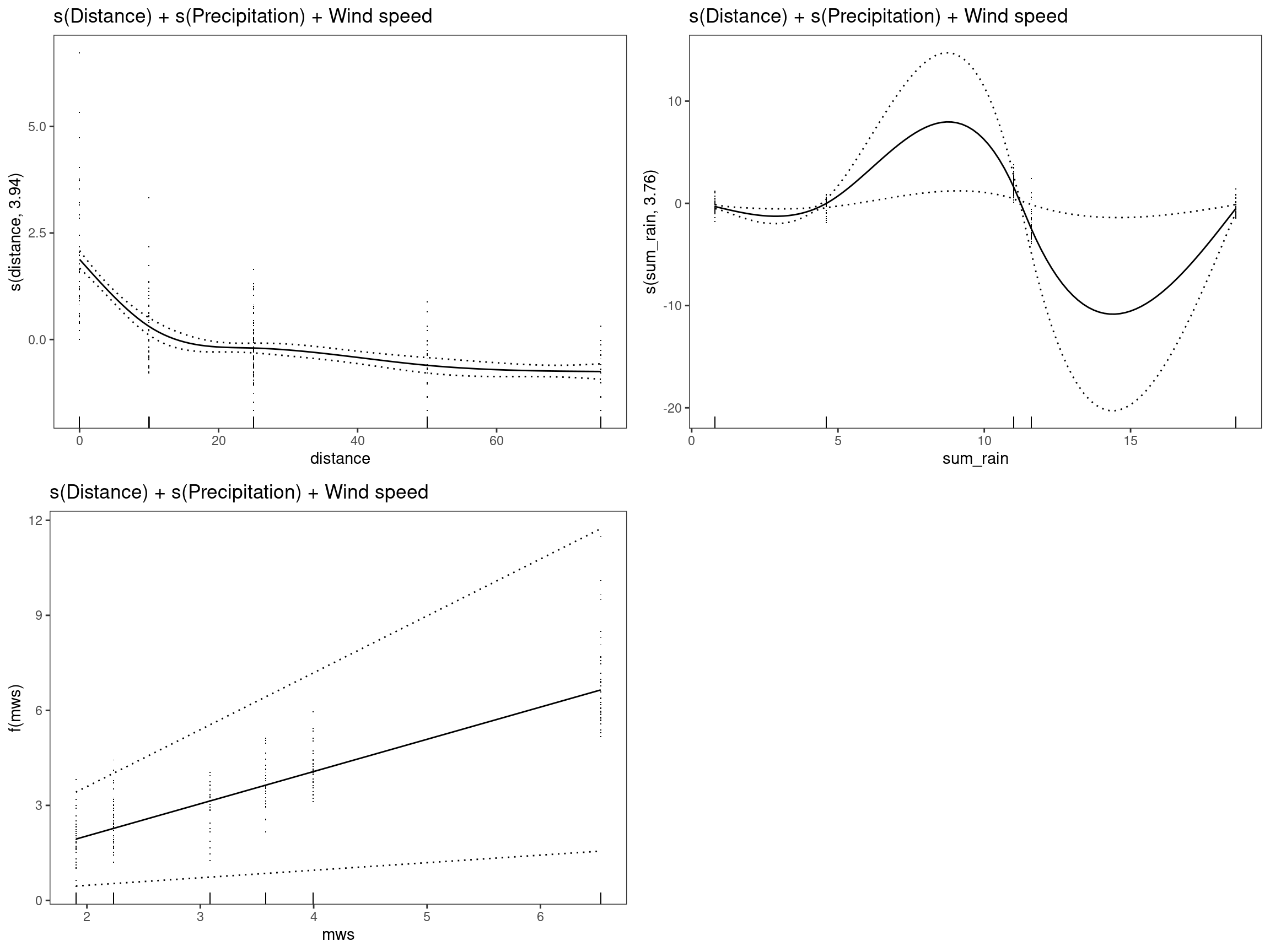
print(p_gam(x = getViz(mod10)) +
         ggtitle("s(Distance) + s(Precipitation) + Wind speed"),
      pages = 1)

mod11 - s(Distance) + s(Wind Speed) + s(Precipitation), family = tw()

This is the same as mod8 but using family = tw(), see ?family.mgcv for more on the families. The Tweedie distribution is used where the distribution has a positive mass at zero, but is continuous unlike the Poisson distribution that requires count data. The data visualisation shows clearly that the mean pot count data have this shape.

mod11 <-
   gam(
      m_lesions ~ s(distance, k = 5) + 
         s(mws, k = 5) + 
         s(sum_rain, k = 5),
      data = dat,
      family = tw()
   )

summary(mod11)
## 
## Family: Tweedie(p=1.044) 
## Link function: log 
## 
## Formula:
## m_lesions ~ s(distance, k = 5) + s(mws, k = 5) + s(sum_rain, 
##     k = 5)
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.22823    0.04098  -5.569 5.39e-08 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##               edf Ref.df       F p-value    
## s(distance) 3.496  3.855 123.776 < 2e-16 ***
## s(mws)      1.992  2.092   0.824 0.45080    
## s(sum_rain) 2.812  2.879   5.493 0.00168 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.674   Deviance explained = 61.2%
## -REML = 309.96  Scale est. = 0.36397   n = 334
print(p_gam(x = getViz(mod11)) +
   ggtitle("s(Distance) + s(Wind Speed) + s(Precipitation), family = tw()"),
   pages = 1)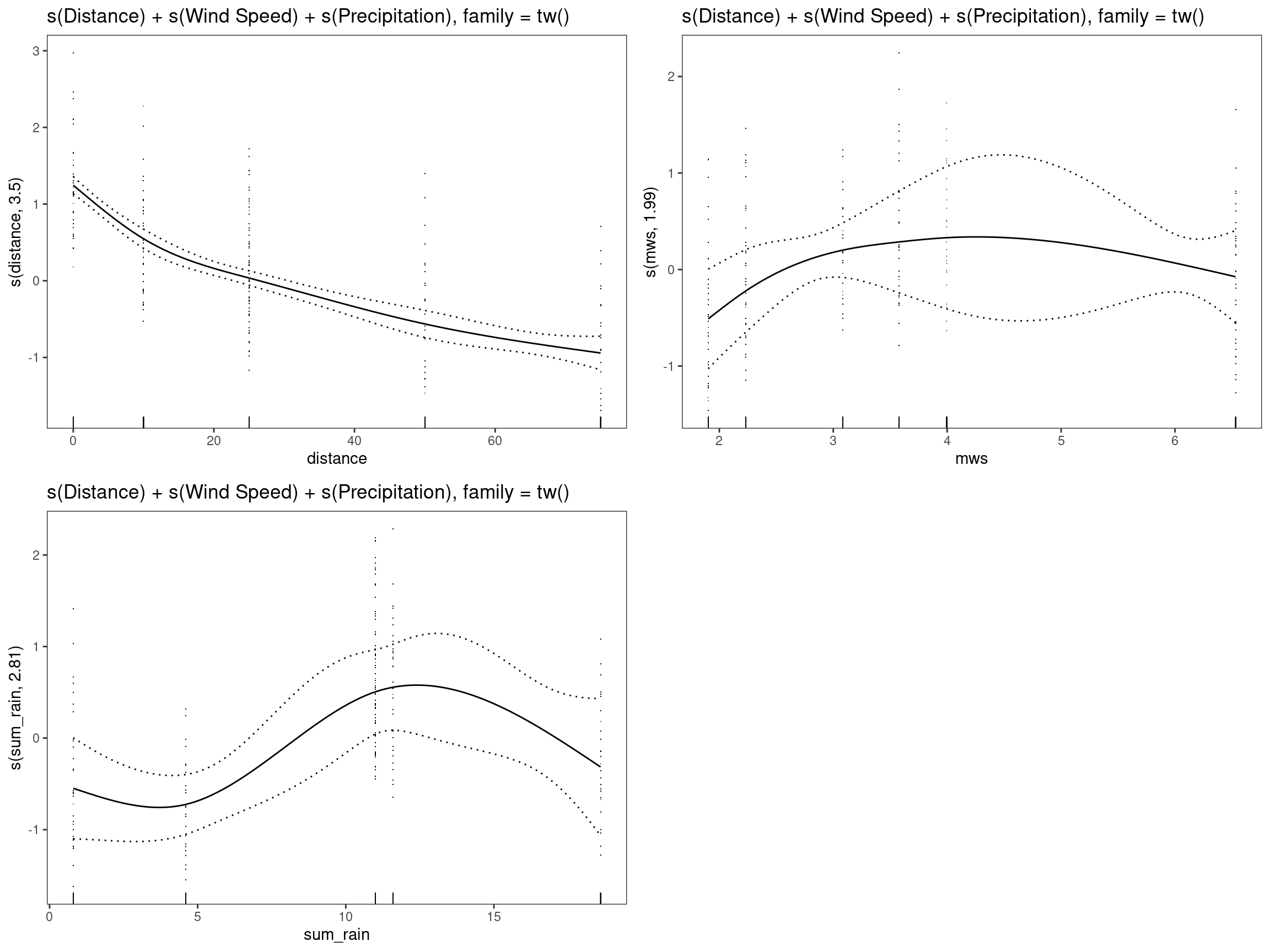

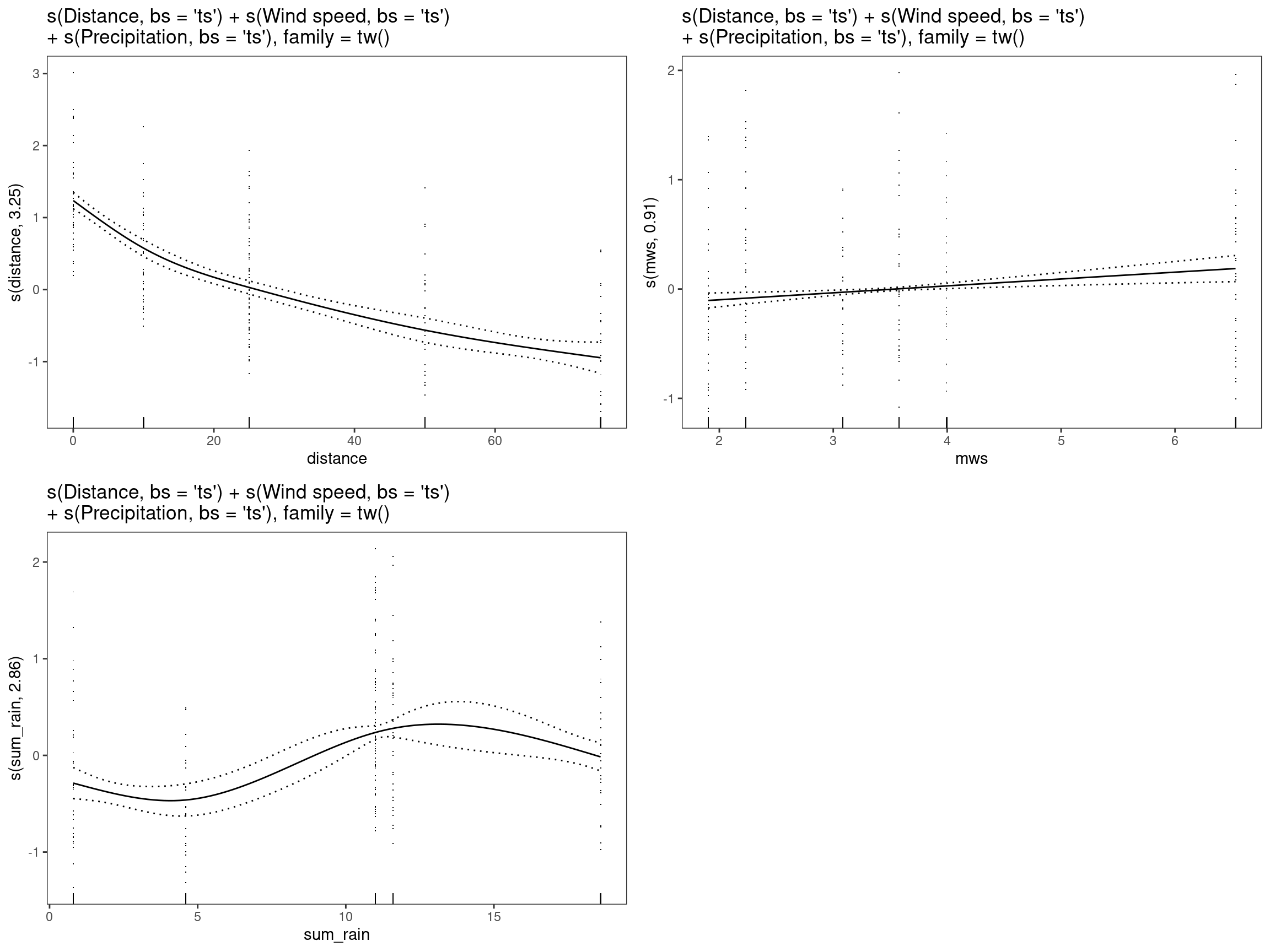
mod12 - s(Distance, bs = “ts”) + s(Precipitation, bs = “ts”) Wind speed, family = tw()

Try using wind speed as a linear predictor only.

mod12 <-
   gam(
      m_lesions ~ s(distance, k = 5, bs = "ts") + 
         s(mws, k = 5, bs = "ts") + 
         s(sum_rain, k = 5, bs = "ts"),
      data = dat,
      family = tw()
   )

summary(mod12)
## 
## Family: Tweedie(p=1.044) 
## Link function: log 
## 
## Formula:
## m_lesions ~ s(distance, k = 5, bs = "ts") + s(mws, k = 5, bs = "ts") + 
##     s(sum_rain, k = 5, bs = "ts")
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.22200    0.04089   -5.43 1.11e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##                edf Ref.df       F p-value    
## s(distance) 3.2481      4 117.664 < 2e-16 ***
## s(mws)      0.9088      4   2.403 0.00027 ***
## s(sum_rain) 2.8645      4  15.752 < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.657   Deviance explained =   60%
## -REML = 319.36  Scale est. = 0.36504   n = 334
print(
   p_gam(x = getViz(mod12)) +
      ggtitle(
         "s(Distance, bs = 'ts') + s(Wind speed, bs = 'ts')\n+ s(Precipitation, bs = 'ts'), family = tw()"
      ),
   pages = 1
)

mod13 - s(Distance, bs = “ts”) + s(Wind speed, bs = “ts”) + s(Precipitation, bs = “ts”), family = tw() 

mod13 <-
   gam(
      m_lesions ~ s(distance, k = 5, bs = "ts") + 
         s(mws, k = 5, bs = "ts") + 
         s(sum_rain, k = 5, bs = "ts"),
      data = dat,
      family = tw()
   )

summary(mod13)
## 
## Family: Tweedie(p=1.044) 
## Link function: log 
## 
## Formula:
## m_lesions ~ s(distance, k = 5, bs = "ts") + s(mws, k = 5, bs = "ts") + 
##     s(sum_rain, k = 5, bs = "ts")
## 
## Parametric coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -0.22200    0.04089   -5.43 1.11e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##                edf Ref.df       F p-value    
## s(distance) 3.2481      4 117.664 < 2e-16 ***
## s(mws)      0.9088      4   2.403 0.00027 ***
## s(sum_rain) 2.8645      4  15.752 < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.657   Deviance explained =   60%
## -REML = 319.36  Scale est. = 0.36504   n = 334
print(
   p_gam(x = getViz(mod13)) +
      ggtitle(
         "s(Distance, bs = 'ts') + s(Wind speed, bs = 'ts')\n+ s(Precipitation, bs = 'ts'), family = tw()"
      ),
   pages = 1
)

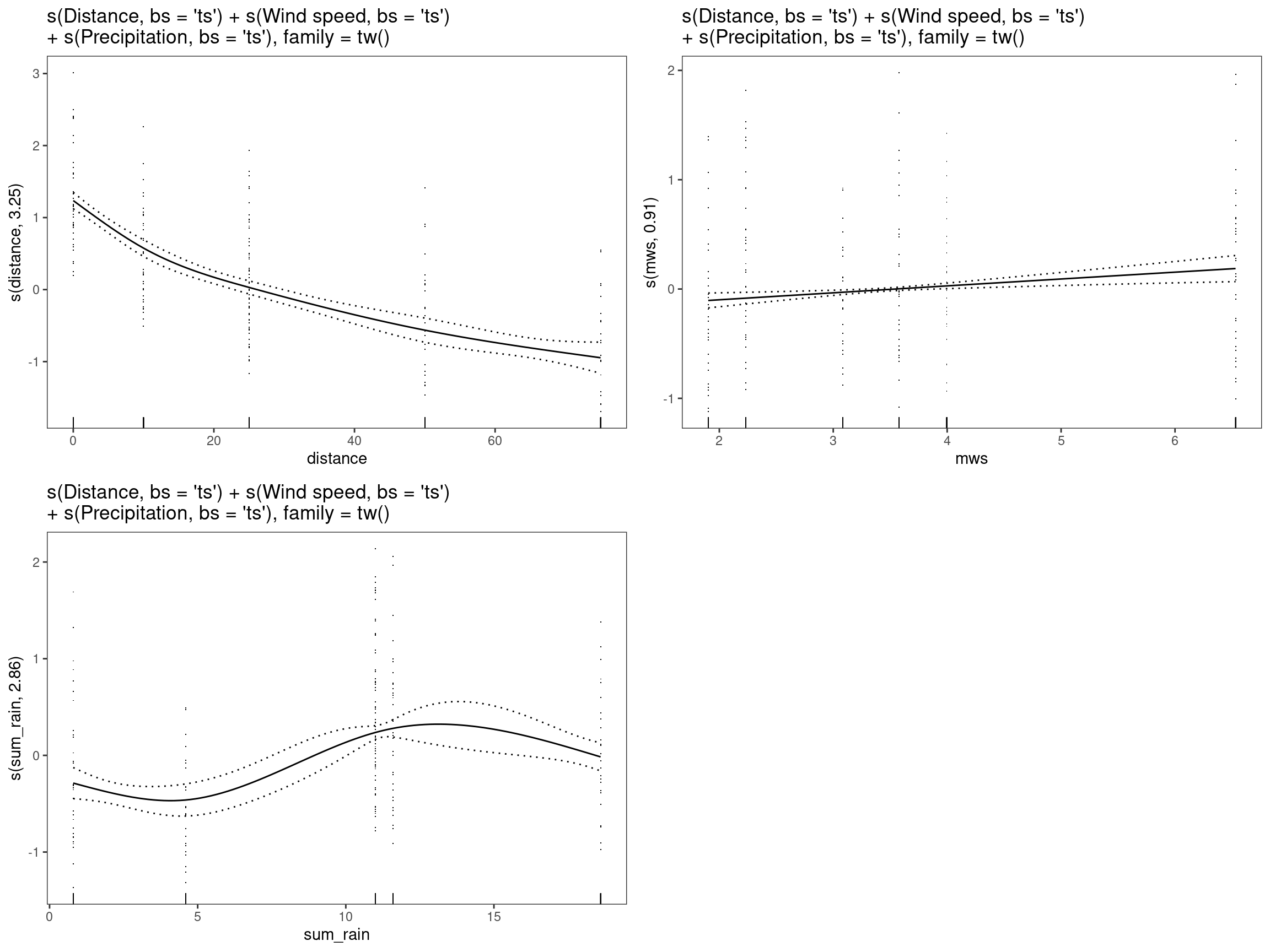
This model, same structure as mod11, uses thin-plate splines to shrink the coefficients of the smooth to zero when possible.

Compare the Models

AIC, BIC 

models <- list(mod1 = mod1,
               mod2 = mod2,
               mod3 = mod3,
               mod4 = mod4,
               mod5 = mod5,
               mod6 = mod6,
               mod7 = mod7,
               mod8 = mod8,
               mod9 = mod9,
               mod10 = mod10,
               mod11 = mod11,
               mod12 = mod12,
               mod13 = mod13
               )
map_df(models, glance, .id = "model") %>%
   arrange(AIC)
## # A tibble: 13 × 8
##    model    df logLik   AIC   BIC deviance df.residual  nobs
##    <chr> <dbl>  <dbl> <dbl> <dbl>    <dbl>       <dbl> <int>
##  1 mod11  9.30  -288.  599.  644.     141.        325.   334
##  2 mod12  8.02  -293.  608.  649.     145.        326.   334
##  3 mod13  8.02  -293.  608.  649.     145.        326.   334
##  4 mod8   9.80  -392.  805.  847.     204.        324.   334
##  5 mod10  9.70  -392.  806.  846.     205.        324.   334
##  6 mod6   9.86  -392.  806.  847.     204.        324.   334
##  7 mod7   8.85  -394.  808.  845.     207.        325.   334
##  8 mod9   8.84  -396.  812.  849.     210.        325.   334
##  9 mod4   6.93  -411.  837.  868.     229.        327.   334
## 10 mod3   5.93  -416.  846.  873.     236.        328.   334
## 11 mod2   5.93  -417.  848.  874.     237.        328.   334
## 12 mod5   5.93  -417.  848.  874.     237.        328.   334
## 13 mod1   4.93  -424.  860.  883.     248.        329.   334

R2 

enframe(c(
   mod1 = summary(mod1)$r.sq,
   mod2 = summary(mod2)$r.sq,
   mod3 = summary(mod3)$r.sq,
   mod4 = summary(mod4)$r.sq,
   mod5 = summary(mod5)$r.sq,
   mod6 = summary(mod6)$r.sq,
   mod7 = summary(mod7)$r.sq,
   mod8 = summary(mod8)$r.sq,
   mod9 = summary(mod9)$r.sq,
   mod10 = summary(mod10)$r.sq,
   mod11 = summary(mod11)$r.sq,
   mod12 = summary(mod12)$r.sq,
   mod13 = summary(mod13)$r.sq
)) %>%
   arrange(desc(value))
## # A tibble: 13 × 2
##    name  value
##    <chr> <dbl>
##  1 mod11 0.674
##  2 mod12 0.657
##  3 mod13 0.657
##  4 mod8  0.566
##  5 mod6  0.566
##  6 mod10 0.566
##  7 mod7  0.562
##  8 mod9  0.557
##  9 mod4  0.519
## 10 mod3  0.504
## 11 mod2  0.502
## 12 mod5  0.502
## 13 mod1  0.482

NOTE The original work had an anova.gam() to compare the models. Somehow, somewhere it seems that changes have been made and current versions of the R packages don’t allow an ANOVA comparison for GAMs that use family = tw(), so this portion has been removed from this vignette. -ahs 2024-04-28

Check Best Model Fit

mod11 - s(Distance) + s(Wind Speed) + s(Precipitation), family = tw() 

mod11_vis <- getViz(mod11)
check(mod11_vis,
      a.qq = list(method = "tnorm", 
                  a.cipoly = list(fill = "light blue")), 
      a.respoi = list(size = 0.5), 
      a.hist = list(bins = 10))
## 
## Method: REML   Optimizer: outer newton
## full convergence after 8 iterations.
## Gradient range [-4.288874e-07,2.610557e-07]
## (score 309.9554 & scale 0.3639671).
## Hessian positive definite, eigenvalue range [0.3685077,2978.832].
## Model rank =  13 / 13 
## 
## Basis dimension (k) checking results. Low p-value (k-index<1) may
## indicate that k is too low, especially if edf is close to k'.
## 
##               k'  edf k-index p-value  
## s(distance) 4.00 3.50    0.87    0.02 *
## s(mws)      4.00 1.99    0.98    0.51  
## s(sum_rain) 4.00 2.81    1.00    0.65  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1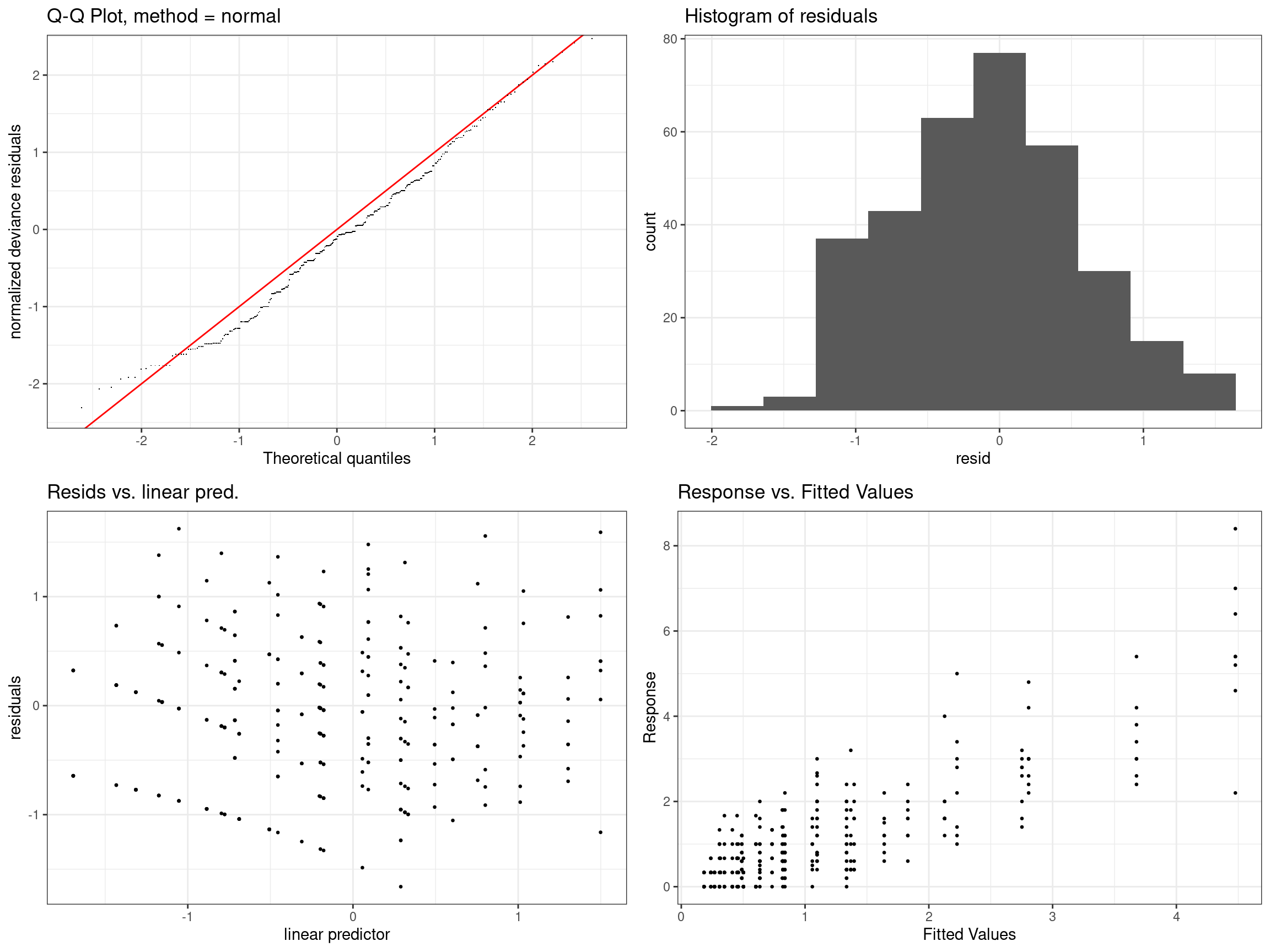

# generate a new plot.gam object just for the publication (no main title)
p11 <- p_gam(x = getViz(mod11))

# save png and eps files
png(
   file = here::here("man/figures", "Fig1.png"),
   width = 640,
   height = 640,
   units = "px",
   pointsize = 14
)
print(p11, pages = 1)
dev.off()

postscript(file = here::here("man/figures", "Fig1.eps"),
           family = "Arial")
par(mar = c(5, 3, 2, 2) + 0.1)
print(p11, pages = 1)
dev.off()

embed_fonts(
   file = here::here("man/figures", "Fig1.eps"),
   outfile = here::here("man/figures", "Fig1.eps"),
   options = "-dEPSCrop"
)

Thoughts

This model, mod11, m_lesions ~ s(Distance) + s(WindSpeed) + s(Precipitation) - family = tw(), is the best performing model. It cannot be used for predictions, but suitably describes the dispersal data we have on hand with the parameters used. More data would be desirable to increase the value of k as evidenced in the GAM checks.